Python勉強中で備忘録です。今回も内容はそこまで多くなかったですが、少し問題で理解に時間がかかりました。
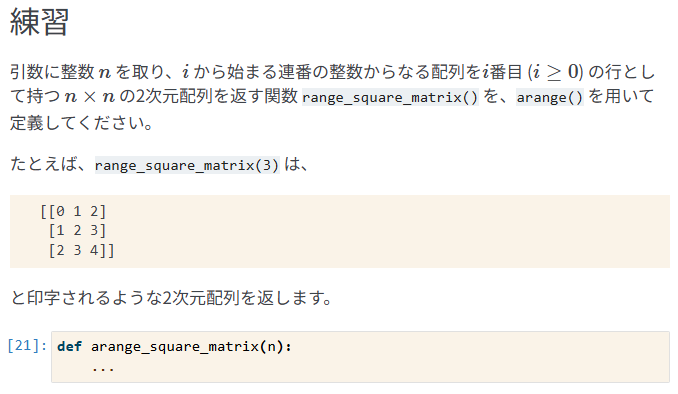
以下の回答を作成したところ、正解となりました。
def arange_square_matrix(n):
a = np.arange(n**2)
x = 0
while x < n**2:
y = x//n
a[x]=x+y-y*n
x += 1
b = a.reshape(n,n)
return b
模範解答は以下の通りでした。「for i in range(n)」をこの位置に使うのはまだ習っていないのでは?

n=3のときは
[
np.arange(0,3),
np.arange(1,4),
np.arange(2,5)
]
*↑[ np.arange(0,3), np.arange(1,4), np.arange(2,5) ]と一緒見え方が違うだけ。
すなわち
[
array([0,1,2]),
array([1,2,3]),
array([2,3,4])
]
こういった1次元配列が連続したリストをnp.arrayで2次元配列でまとめているという理解のよう。これもChatGPTで理解できましたが、テキストだけ見ても分からなそうな。この問題は不親切な気がしました。色々勉強にはなりましたが。
ChatGPTの模範解答は以下の通りでした。行(横ベクトル)+列(縦ベクトル)を足すとこういう計算になるのは知りませんでした。高校で習わなかった気がします。でも解答としては分かりやすいですね。


⇒numpy.dot()と numpy.matmul() の違いが良く分からなかったのでChatGPTに説明してもらいました。
✅ 一番大きな違い
| 関数 | 主な用途 |
|---|---|
numpy.dot() | 「内積」寄りの歴史的関数(やや挙動が多用途) |
numpy.matmul() | 「行列積」専用(@ 演算子と同じ) |
🔹 1次元ベクトル同士
a = np.array([1,2,3])
b = np.array([4,5,6])
dot
np.dot(a, b)
→ 32(内積)
matmul
np.matmul(a, b)
→ 32(同じ)
👉 ここは同じ
🔹 2次元配列(普通の行列)
A = np.array([[1,2],[3,4]])
B = np.array([[5,6],[7,8]])
dot
np.dot(A, B)
matmul
np.matmul(A, B)
👉 どちらも普通の行列積になる
🔹 3次元以上で違いが出る
ここが重要 ⚠️
dot の挙動(ちょっとクセがある)
np.dot(A, B)
- 最後の軸とその前の軸を使って計算
- 高次元だと やや直感的でない
matmul の挙動(直感的)
np.matmul(A, B)
- 最後の2軸を「行列」として扱う
- 前の軸は「バッチ処理」扱い
つまり:
👉 ディープラーニングや線形代数的には matmul が自然
🔹 1次元 × 2次元 の違い
これも少し違う。
dot
np.dot(a, A)
→ OK
matmul
np.matmul(a, A)
→ ベクトルを行列とみなして計算
概ね同じだが、
matmulは「行列の世界」に寄せて考える。
🔹 @ 演算子
A @ B
これは
np.matmul(A, B)
と同じ。
🔹 まとめ
✔ 基本的な使い分け
- ベクトル内積 →
dot - 行列積 →
matmulまたは@
✔ 実務的おすすめ
👉 今から書くなら @(=matmul)を使うのが普通
理由:
- 挙動が明確
- 高次元で自然
- 新しい書き方
🔹 一言でまとめると
dot = 古くて多用途
matmul = 純粋な行列積
@ = いま主流⇒分かりにくいですが、とりあえず基本的には行列積はmatualを使うのが良いと思いました。

⇒ノルムはベクトルの大きさ(長さ)。


コメント